Vizsgáljuk meg egy kitöltött normál szudokutábla soraiban a szomszédos, együttesen kétjegyű számot alkotó számokat. Az alábbi ábrában tehát ezek a számok: 68, 85, 52, 21, 17, 79, 93, 34, 13, 34, 49, ...stb. Bizonyára feltűnt már Neked is, hogy ezen számok közül néhányan többször is szerepelnek.



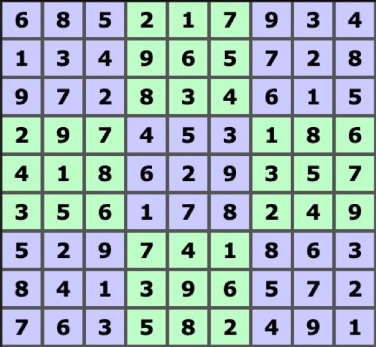
Ebben a minta-táblában például a 34-es az első három sor mindegyikében megtalálható. Sőt, az összesen 72 szám közül csak 17 szerepel szimplán (15, 21, 31, 39, 45, 46, 53, 58, 62, 68, 76, 78, 79, 83, 84, 85, 91) és a többi 23 pedig duplán, illetve triplán.

Ezzel a gondolattal kapcsolatos a mostani feladat.
Sorfolytonosan töltsünk ki egy üres táblát minél több számmal úgy, hogy a szudoku szabályai érvényesüljenek, azaz a soron következő számjegy ne szerepeljen máshol az adott cella sorában, oszlopában vagy kisnégyzetében,
ÉS
ezek a speciális kétjegyű számok se szerepeljenek duplán a táblában.

A játék célja, hogy SORFOLYTONOSAN töltsük fel így a tábla első öt (5) sorát.

Pontozás a 36-odik számjegy (4 sor) beírásakor kezdődik (8 pont), a 41-edik számjegynél +1 pont, a 45-ödik számjegynél +1 pont.
Ne foglalkozzunk azzal, hogy a már félig kitöltött tábla kitölthető lesz-e teljesen, vagy sem! Most csak a már beírt számok játszanak.
Ösztönző felhívás az aktív időszak beküldőihez, akik szeretik a kihívásokat:
- Dicséretet érdemel, aki több mint 46 számjegyet tud beírni a táblába sorfolytonosan, a kétjegyű szabállyal.
- Csillagos dicséretet érdemel, aki a számait a normál szudoku szabályaival teljessé tudja tenni, és be is mutatja ezt a kitöltött tábláját. (Tehát a kiegészítésben már nem kell vizsgálni a kétjegyűeket.)
- Dupla csillagos dicséretet érdemel, aki a kétjegyes szabállyal is ki tudja a teljes táblát tölteni.