|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Friss fórum:
|
|
|
|
A hét kérdése:
Jelentkezz be a heti kérdéshez!
|
|
|
|
Legolvasottabbak:
|
|
|
Elutasított feladványok
Hirdetés
| kadar |
kadar (748400) |2021.12.14 10:40 | | 748401. |

| |
Persze azért pontosan kell számolni:
13+6/2-1=15 (és nem 14) |
|
| kadar |
2021.12.14 10:32 | | 748400. |

| |
A mai feladat túl könnyűre sikeredett. Ezért, akinek hiányérzete lenne, az gondolkozzon el Ödönke feladatán:
Ödönke azt mondja, hogy egy olyan sokszög területét, melynek csúcsai a négyzetrács csúcspontjaira illeszkednek, az alábbi képlettel könnyedén ki tudja számolni:
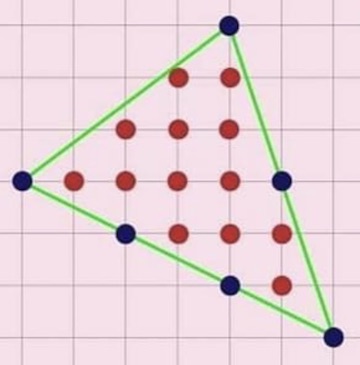
A belső (piros) csúcspontok azám + a sokszög oldalaira illeszkedő csúcspontok számának a fele-1 = a sokszög területe.
A fenti ábra szerint 13+6/2-1=14 egységnyi a sokszög területe.
Ödönke jelentős pénzjutalmat ajánlott fel annak, aki egy olyan sokszöget mutat neki, amire ez nem igaz. |
|
| mutterka |
szedit24 (748204) |2021.11.12 17:02 | | 748205. |

| |
Ne sértődj meg, én sem sértődtem meg. Csupán elnyomtam egy sóhajt, az talán nem baj.
A megoldással tegnap éjjel készen voltam már és az "örömét" is tapasztaltam.
Megszólalásom lényege inkább a feladat dicsérete volt. |
|
| szedit24 |
kadar (748203) |2021.11.12 16:47 | | 748204. |

| |
Természetesen kiokoskodtam 😀, osztahatósági szabályokkal elég hamar célba értem. Nem írom le ide a részleteket, ne okozzak bajt. |
|
| kadar |
szedit24 (748202) |2021.11.12 16:29 | | 748203. |

| |
Igen, én mondtam, hogy ide kérem a megoldást. Valójában nem gondoltam, hogy lesz rá érdeklődő. Bocsánat kedves Mutterka!
Annyit még mondj el, hogy megkerested ezt a számot, vagy kiokoskodtad?
|
|
| szedit24 |
mutterka (748201) |2021.11.12 16:11 | | 748202. |

| |
Szia, ne haragudj, ha elvettem az örömödet. De: 1. Ha gyorsasági versenynek szántam volna, tegnap kiírtam volna, vártam, nem volt érdeklődés. 2. Direkt nem részleteztem a megoldást. Meg amúgy is, attól, hogy látni a végeredményt még örömet tud okozni az oda vezető út, nyugodtan dolgozhattál volna tovább vele. 3. Kadar azt írta, itt a fórumban várja a megoldásokat. Vagy ezt félreértettem?
Mindenesetre tényleg bocsánat, máskor többet várok. |
|
| mutterka |
szedit24 (748199) |2021.11.12 14:22 | | 748201. |

| |
Kár, hogy kiírtad. Dolgoztam vele én is, de nem gondoltam, hogy gyorsasági verseny.
Már mindegy, veszett fejsze nyele.
Szerintem is jó kis feladat, egyedül is megállta volna a helyét. |
|
| szedit24 |
kadar (748197) |2021.11.12 08:11 | | 748199. |

| |
Szia! Osztható kell legyen: 625, 11, 9. Egy ilyen szám van: 5618064375
Szia! |
|
| kadar |
2021.11.11 19:55 | | 748197. |

| |
A mai Prímek világa című feladatnak volt egy negyedik pontja, amit végül kivettem belőle. De ha valakinek kedve van megfejteni (itt a fórumban), azt szívesen várom.
Móricka azt mondja hogy van öt db olyan (nem feltétlenül különböző) a,b,c,d,e számjegy, hogy az a61b064cde osztható lesz 61875-el! Bár ez nem prím, de azért ezt is ajánlja somolyogva, a prímszámkutatók figyelmébe. Igaza lehet? |
|
| grisenyka |
2020.01.04 05:58 | | 742297. |

| |
Ez egy betűrejtvény lenne. Én döntöttem úgy, hogy nem teszem be feladványnak. De ide elfér. Várom az ötleteket:
Z
|
|
|
|
|