|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Friss fórum:
|
|
|
|
A hét kérdése:
Jelentkezz be a heti kérdéshez!
|
|
|
|
Legolvasottabbak:
|
|
|
Matek
Hirdetés
| mbela |
2025.05.12 14:44 | | 756487. |

| |
Geometria
Nagy kör sugara R, kis kör sugara r
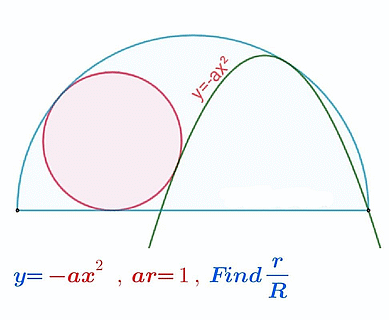
parabola kör érintő
|
|
| titok111 |
2025.02.25 14:19 | | 755954. |

| |
És ma van háremszerűen kell elképzelni? Azaz ha engedélyezett a többférjüség, akkor 1 nőnek legyen 7 férje. Ennek a nőnek 7 gyereke van, de a férfiaknak is 7, trhát korábbi 7×6 gyerek+7+s 6 szingli nő 6×7 gyereke. |
|
| Sandviking |
grisenyka (755949) |2025.02.25 13:55 | | 755953. |
| |
Ez azért eléggé zavaróan van megfogalmazva.
Normális esetben 14 felnőtt és 49 gyermek = 63 fő.
De lehet, hogy minden nő már volt házas mindegyik férfival, s darabonként csak 1-et szültek, akkor csak 21 fő. |
|
| grisenyka |
2025.02.25 00:21 | | 755949. |

| |
7 nőnek van 7 férje. Minden nőnek és férfinek van 7 gyereke. Hányan vannak összesen?
|
|
| dingidungi |
2023.05.03 13:36 | | 752761. |

| |
Érdekes dolog elmélyülni a 'végtelen' meglehetősen rejtélyes fogalmában. Sok vicces dolog, paradoxon is kiderülhet. Példa a végtelen szobájú szálloda, minden szoba foglalt. Jön egy új vendég. Elhelyezhető-e? Igen. Jön végtelen számú új vendég. Elhelyezhetőek-e? Igen. És jön a takarítónő. Első szobára szán 1 percet, másodikra fél percet, harmadikra negyed percet és így tovább. Belátható, hogy akkor 2 perc elég, hogy kitakarítson mindent. Igen ám, de ha végzett (végzett?) akkor vajon hogyan jön vissza? Erre nincsen értelmezhető válasz.  Netflix->Dokumentumfilmek->Utazás a végtelenbe. Netflix->Dokumentumfilmek->Utazás a végtelenbe. |
|
| Mesti1 |
2023.04.05 23:34 | | 752605. |

| |
Ha beírjuk az Excel-be:
=(36/3*(8-6))/6 a cellában 4 lesz az eredmény |
|
| titok111 |
2023.03.30 09:51 | | 752551. |

| |
Fejjel lefelé nézitek! Valójában -1e a megoldás. |
|
| mutterka |
hata (752548) |2023.03.29 19:48 | | 752549. |

| |
Ha "rendes formában" írod le, akkor a
(8-9) tényező a számlálóba kerül, a 36 szorzójának. |
|
| hata |
2023.03.29 19:01 | | 752548. |

| |
És ha rendes formában írjuk fel?
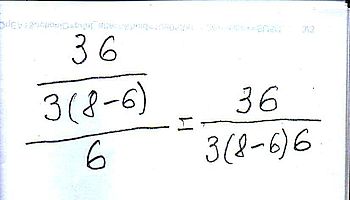 |
|
| Tucatka |
2023.03.29 18:34 | | 752547. |

| |
Szerintem is 4. De nem én vagyok az internet :-) |
|
| hata |
2023.03.28 19:39 | | 752540. |

| |
Én is 4-et látok.
De lehet, hogy a zárójel kicsit bezavar a képbe.
Ha rendesen lenne felírva, talán egyértelmű lenne.
|
|
| pantharei01 |
2023.03.28 11:05 | | 752536. |

| |
Vagy, ahogy Hofi mondta: kivonom a péntekből a 90-et...:-)) |
|
| pantharei01 |
2023.03.28 11:04 | | 752535. |

| |
Szerintem 3
De én ehhez (se) nem értek..:-))) |
|
| cslaci |
2023.03.28 10:33 | | 752534. |

| |
Ha egy műveletsorban kizárólag összeadás és kivonás, vagy pedig kizárólag szorzás és osztás van, akkor balról jobbra haladunk. |
|
| mutterka |
2023.03.27 19:35 | | 752528. |

| |
Én is a 4-re szavazok! |
|
| hata |
2023.03.27 19:01 | | 752525. |

| |
Szerinted mennyi az annyi?

Két táborra szakadt az internet |
|
| tark |
portugal (751869) |2023.01.02 12:48 | | 751914. |

| |
Talán erre gondolt fejben ocotillo pár hozzászólással előbb:
Felhasználva, hogy:
7*7*7 + 17 = 360 = 6!/2
(a+b)(a-b) = a^2 - b^2
2023 = 7*17*17 (nem csak portugal szerint)
(7*7*7 + 17)(7*7*7 - 17) = 7^6 - 17^2
A mindkét oldali hétszeres volt az állítás.
(A 2 szorzó is megvan, mert a (7*7*7 - 17) páros.)
(Jut eszembe, visszatekintés a 2020-as karácsonyi magyarázat-botladozásra:
A végtelen határértékre külön definíció dukál, Matematika Úr sem tudja belesúvasztani a véges határérték definíciójába. Persze, hogy nekem sem sikerült, az emlékezetem volt rövidebb a kelleténél.) |
|
| dingidungi |
dingidungi (751865) |2022.12.30 11:47 | | 751870. |

| |
Egy másik történet jutott eszembe, meghehet klasszikus a sztori. Természetes számok, mindegyiknek van valamely olyan jellemzője, amellyel kiválik a többiek közül. Például 2, aki egyetlen páros prímszám. Mindegyikre ki lehet találni valamit, amitől különbözik a többiektől, amitől érdekes. Képzeletben osszuk el a számhalmazt két részre, egyikőjük érdekes, másik nem. Ebben az esetben az érdektelenek halmazában kell legyen egy legkisebb. Aki azért érdekes, mert a legkisebb érdektelen q.e.d.  |
|
| portugal |
2022.12.30 11:07 | | 751869. |

| |
2023=7*17*17 |
|
| dingidungi |
2022.12.30 08:26 | | 751865. |

| |
Kíváncsiságból ránéztem, 2023 nem prímszám, 2023=119*17. Izgalmasabb lenne, bár biztosan így is lehet kiötleni mindenféle furmányokat. Ha minden igaz, legközelebb 2027 lesz, arra még kicsit várni kell.  |
|
| ocotillo |
hata (751861) |2022.12.30 05:50 | | 751864. |

| |
Feladványtól függ, 2023 meg minden lehet 
Ez a 7! faktoriális kedves ötlet és furmányos agy, aki kiötölte. Ellenőrizni már fejben is lehet. |
|
| hata |
(751858) |2022.12.29 22:00 | | 751861. |

| |
Akkor én sem leszek népszerű ha a 2023-hoz kapcsolódó két feladatom terítékre kerül?
|
|
|
|
|